AVL Tree and B Tree

AVL Tree

AVL tree is a binary search tree in which the difference of heights of left and right subtrees of any node is zero or equal to one. 

The technique of balancing the height of binary trees was developed by Adelson, Velskii, and Landi and hence given the short form as AVL tree or Balanced Binary Tree.

Advantages

Since AVL are height-balanced trees, operations such as insertion and deletion have a low time complexity.

AVL tree checks the height of the left and the right sub-trees and assures that the difference is not more than 1. This difference is usually called as the Balance Factor

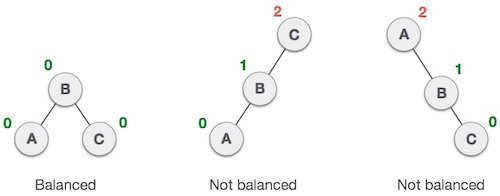
In the second tree, the left subtree of C has height 2 and the right subtree has height 0, so the difference is 2. In the third tree, the right subtree of A has height 2 and the left is missing, so it is 0, and the difference is 2 again. AVL tree permits difference (balance factor) to be only 1.

Balance Factor = height(left sub-tree) - height(right sub-tree)

Insertion

Step 1: First, insert a new element into the tree using BST's (Binary Search Tree) insertion logic.

Step 2: After inserting the elements you have to check the Balance Factor of each node.

Step 3: When the Balance Factor of every node will be found like 0 or 1 or -1 then the algorithm will proceed for the next operation.

Step 4: When the balance factor of any node comes other than the above three values then the tree is said to be imbalanced. Then perform the suitable Rotation to make it balanced and then the algorithm will proceed for the next operation.

There are four kinds of rotation:

1. Left Rotate

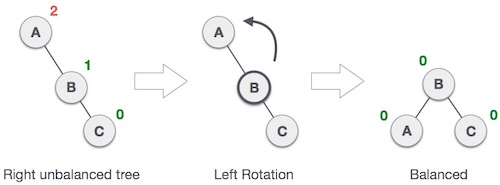
2. Right Rotate

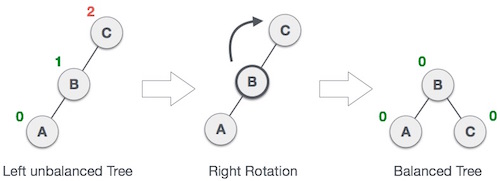
3. Left Right Rotate

4. Right Left Rotate

Deletion

Step 1: Firstly, find that node where k is stored

Step 2: Secondly delete those contents of the node (Suppose the node is x)

Step 3: Claim: Deleting a node in an AVL tree can be reduced by deleting a leaf. There are three possible cases:

• When x has no children then, delete x
• When x has one child, let x' becomes the child of x.
• Notice: x' cannot have a child, since subtrees of T can differ in height by at most one :
  • then replace the contents of x with the contents of x'
  • then delete x' (a leaf)
• Step 4:  When x has two children,
  • then find x's successor z (which has no left child)
  • then replace x's contents with z's contents, and
  • delete z

In all of the three cases, you will end up removing a leaf.

B Tree

There is a special type of tree called a B Tree in which a node contains more than one value/key and more than two children.

B-Tree of Order m has the following properties:

• Property #1 - All leaf nodes must be at same level.
• Property #2 - All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.
• Property #3 - All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.
• Property #4 - If the root node is a non leaf node, then it must have atleast 2 children.
• Property #5 - A non leaf node with n-1 keys must have n number of children.
• Property #6 - All the key values in a node must be in Ascending Order.

For example, B-Tree of Order 4 contains a maximum of 3 key values in a node and maximum of 4 children for a node.

Search Operation in B-Tree

• Step 1 - Read the search element from the user.
• Step 2 - Compare the search element with the first key value of the root node in the tree.
• Step 3 - If both are matched, then display "Given node is found!!!" and terminate the function
• Step 4 - If both are not matched, then check whether the search element is smaller or larger than that key value.
• Step 5 - If the search element is smaller, then continue the search process in left subtree.
• Step 6 - If the search element is larger, then compare the search element with next key value in the same node and repeat steps 3, 4, 5, and 6 until we find the exact match or until the search element is compared with last key value in the leaf node.
• Step 7 - If the last key value in the leaf node is also not matched then display "Element is not found" and terminate the function.

Insertion Operation in B-Tree

In a B-Tree, a new element must be added only at the leaf node. That means, the new keyValue is always attached to the leaf node only. The insertion operation is performed as follows:

• Step 1 - Check whether the tree is Empty.
• Step 2 - If the tree is Empty, then create a new node with a new key-value and insert it into the tree as a root node.
• Step 3 - If the tree is Not Empty, then find the suitable leaf node to which the new key value is added using Binary Search Tree logic.
• Step 4 - If that leaf node has an empty position, add the new key value to that leaf node in ascending order of key-value within the node.
• Step 5 - If that leaf node is already full, split that leaf node by sending middle value to its parent node. Repeat the same until the sending value is fixed into a node.
• Step 6 - If the splitting is performed at the root node then the middle value becomes new root node for the tree and the height of the tree is increased by one.